펜윅트리

• 최하위 켜져있는 비트를 기반으로 트리를 만들어 동적배열에서 구간합을 효율적으로 구할 수 있는 자료구조
• 구간 합을 구하는 쿼리, 값 갱신 작업을 O(logN) 만에 가능
• 인덱스가 1부터 시작
• 최하위 켜져있는 비트 = idx & -idx
• 3(11)의 최하위 켜저있는 비트는 1(1), 4(100)의 최하위 켜져있는 비트는 4(100)

작동 원리

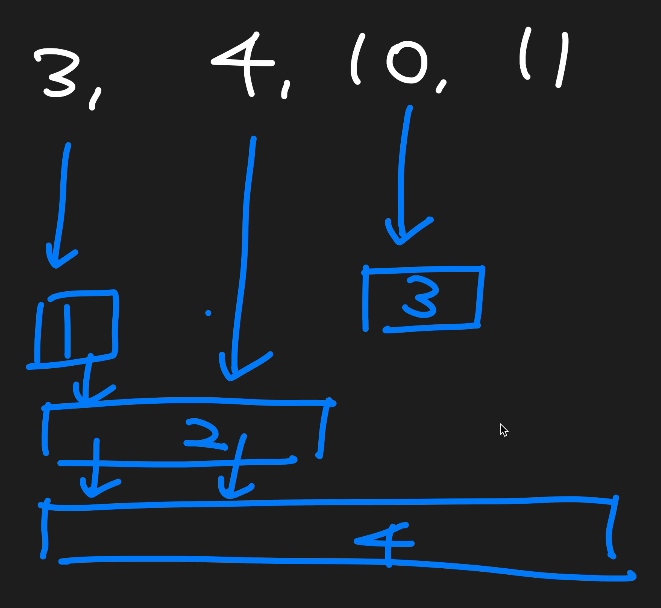
• 각 블록에는 배열의 합들이 저장되어 있음

1. 구간 합

• 1~2 의 합 = 2번 블록
• 2~3 의 합 = 2번 + 3번 블록

2. 값 갱신

• 3번 배열 값에 +val
• 3번 배열 값은 블록 3, 4번에 영향을 미침
• 그래서 우선 블록 3에 +val
• 다음 인덱스 += (현재 인덱스)&-(현재 인덱스)
• binary : 100 = 11 + (11 & 01)
• 다음 인덱스인 4번 블록에 +val

코드

data = [3, 4, 10, 11]
n = len(data)
tree = [0] * (n + 1) # 1번 인덱스부터 시작해야 하므로


def range_update(index, value):
    global tree
    while index < len(tree):
        tree[index] += value
        index += index & -index


def _sum(index):
    ret = 0
    while index > 0:
        ret += tree[index]
        index -= index & -index
    return ret


def range_query(left, right):
    return _sum(right) - _sum(left - 1)


for i in range(n):
    range_update(i + 1, data[i])

print(tree) # [0, 3, 7, 10, 28]

print(range_query(1, 2)) # 7
print(range_query(2, 4)) # 25

range_update(2, 5)
print(tree) # [0, 3, 12, 10, 33]

print(range_query(1, 2)) # 12
print(range_query(2, 4)) # 30